This tutorial is meant as an introduction to the problem of trajectory generation. It introduces several ways for modelling the motion of agents in pixel space and proposes several ways of preprocessing data. It follows the structure from its associated GitHub repository. Feel free to skip to the end to see the performance of 2 basic models.

Introduction

The acquisition of neural-based solutions such as Long Shrort-Term Memory [1] has become very common for modelling time series signals in the past few years. Some popular and well established examples include different applications of AI; and namely speech processing [2], language modelling [3], translation [4] among many others. In particular, the idea behind LSTMs is that they are good at mimicing the hidden dynamics behind a given short sequence.

The overall structure of such networks (see the figure bellow, taken from Chris Olah’s blog post which is a great introduction to LSTMs along with Chapter 10 of the book “Deep Learning”) allows us to model each step while taking into account all previously considered ones in a given signal. In the context of text modelling, those signals can be all previously observed words in a given sentence where each step would consist of predicting one word by conditioning on all previously seen words. In this context, LSTMs are good at encapsulating the context behind a given sentence which makes them a good candidate for predicting its continuation.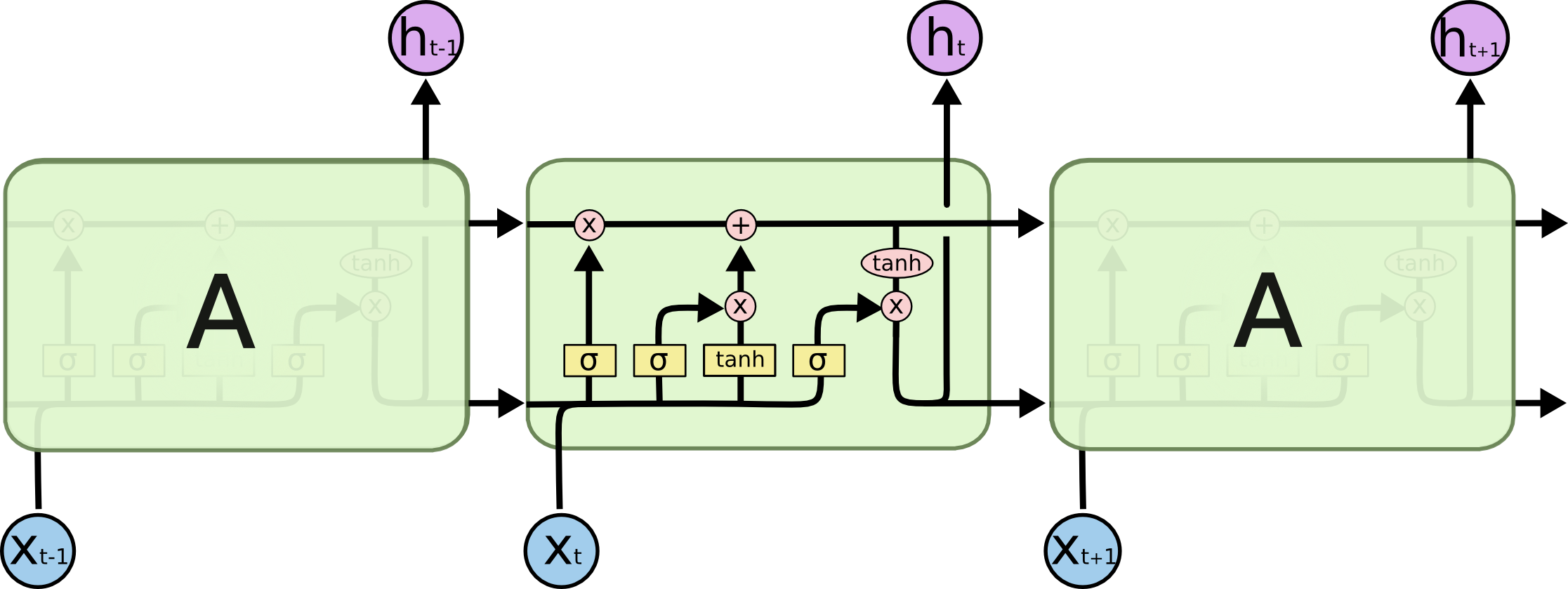

Similarly, we can model the dynamics associated with the motion of pedestrians in crowded scenes, the behaviour of agents in different games, moving cars on a busy road etc. In such cases, the task would be to predict where each considered agent will be after some time. This post is an introduction to the use of LSTMs in such problems.

We will focus on predicting the next few 2D positions (x,y) of pedestrians from annotated videos. We will assume a good understanding of what LSTMs are, the difficulties behind extracting meaningful feature representations as well as basic computer science knowledge, algebra and calculus, and some prior knowledge of using Tensorflow. We aim to conclude with a brief discussion of the pros and cons of using the introduced here use of LSTMS.

Anticipating the position of pedestrians in a given video sequence is often a challenging task even for humans. Motion is often dictated by some unspoken rules that are different across cultures and are in addition interpreted differently by people. For example, when walking in crowded scenes we might aim to avoid collisions with others, but we can also aim to reach someone specific and stop in front of them. In such cases it is relatively difficult for an observer to anticipate what would be the goal of someone walking in the scene in the next 5-10 minutes just by observing but we can relatively easily tell where a pedestrian aims to be in the next 5-10 seconds. Regardless, we often maintain a few hypothesis of where this person will be and thus modelling such motions using purely deterministic approaches (such as simply using standard LSTMs) can be very hard. An alternative solution would be to train a neural network to model the sufficient statistics of the distribution the next step is sampled from.

Initialization

We begin by installing tensorflow and downloading the github code described in this blog post. We then import everything necessary including all datasets we will use for training, followed by assigning all constant variables we will need for training the network.

!pip install tensorflow==1.15.0

!git clone https://github.com/yadrimz/Stochastic-Futures-Prediction.git

Problem Formulation

This work’s focus is on predicting the future motion of an arbitrary number of observed agents (i.e. their behaviour) whose action spaces and objectives are unknown. More specifically, we focus on predicting the two-dimensional motion of agents in video sequences.

We assume we are given a history of two-dimensional position annotations and video frames as a sequence of RGB images. Each agent $a$ ($a \in [1 \ldots A]$, where $A$ is the maximum number of agents in the video) is represented by a state ($s_t^a$) which comprises xy-coordinates at time t, $s_t^a$ = $(x_t,y_t)_a$.

Given a sequence of $obs$ observed states $S = s_{t-obs}, s_{t-obs+1}, \ldots, s_{t-1}, s_{t}$, we will formulate the prediction as an optimisation process, where the objective is to learn a posterior distribution $P(Y \vert S)$, of multiple agents future trajectories $Y$. Here an individual agent’s future trajectory is defined as ($s_t^a = {s_{t+1}^a, s_{t+2}^a, \ldots, s_{t+pred}^a}$) for $pred$ steps ahead for every agent $a$ found in a given frame at time $t$.

import os
import time

%tensorflow_version 1.x

import numpy as np
import tensorflow as tf

import utils.data_tools as data_tools
import utils.visualisation as visualisation
import utils.distributions as distributions

from models.lstm import BasicLSTM
from models.lstm import reset_graph